
La foto que abre esta entrada es bastante popular. Más que por la foto en sí, por una aplicación que permite escribir en la pizarra lo que cada cual quiera. Y, sin embargo, esta foto tiene una historia cuando menos curiosa que nos va a permitir explorar someramente la idea de curvatura y cómo expresarla usando una herramienta matemática tremendamente útil en física, los tensores, a la par que rememorar un momento muy interesante en la historia de la cosmología.
En una época anterior a internet, las fotos de las noticias eran enviadas por las agencias de prensa por correo ordinario urgente a los distintos periódicos. Cada fotografía llevaba anexa su historia escrita por la agencia de noticias adherida a la parte posterior, de esa forma el periódico no tenía que complicarse a la hora elaborar el pie de foto.
La foto de Einstein fue tomada el 14 de enero de 1931 durante su visita al complejo del Observatorio del Monte Wilson en California (Estados Unidos). Sin embargo se hizo pública 24 años después, con motivo de la muerte de Einstein el 18 de abril de 1955. El pie de foto con el que apareció en prensa decía: “Dr. Albert Einstein writes an equation for the density of the Milky Way on the blackboard at the Carnegie Institute, Mt. Wilson Observatory headquarters in Pasadena, Calif., in this Jan. 14,
La historia anexa a la foto que mandó la agencia de noticias podría ayudarnos a desvelar esta posible contradicción. El original es el siguiente (cortesía de Einstein’s World):

Vemos que “density” era originalmente “destiny”. ¿Podría haber ocurrido que el avezado reportero de la agencia de noticias se limitase a reflejar la frase que entendió y le llamó la atención y que, en algún paso intermedio, alguien decidiese que el “destino” no puede expresarse en una ecuación y que lo que quería decir es “densidad”? Podría ser. En cualquier caso, parece más cierto que Einstein lo que hacía era escribir aparentemente sobre la curvatura del espaciotiempo. Pero en realidad estaba considerando el problema de la existencia de la constante cosmológica. Vamos a verlo, que es muy fácil de entender intuitivamente.
Si cortas una naranja por la mitad, quitas la pulpa del interior, e intentas aplanar el hemisferio de piel resultante, terminas rajándolo. Si tratas de aplanar algo con la forma de una silla de montar, como una patata frita (de las de bolsa) revenida, te encuentras con el problema contrario: hay “demasiada” superficie y se te forman pliegues. Si coges, sin embargo, un rollo de papel de cocina y deseas aplanarlo, no hay nada más fácil, con desenrollarlo, listo. Las superficies como las esferas se dice que están curvadas positivamente, las que tienen la forma de una silla de montar que lo están negativamente, y las que son como el papel de cocina son, simplemente, planas (démonos cuenta que son planas en este sentido aunque no estén en un plano). Esto es así porque la curvatura se define en términos de “geometría intrínseca” de una superficie, en la que la distancia se mide en función de los caminos que están dentro de la superficie.
Hay varias formas de hacer precisa esta noción de curvatura y hacerla cuantitativa, de tal manera que a cada punto de la superficie se pueda asociar un número que diga “cómo de curvada” está en ese punto. Para poder hacer esto es necesario que se cumplan determinadas condiciones matemáticas que permitan determinar las longitudes de los caminos, es lo que se llama una métrica riemanniana. La noción de curvatura puede ser generalizada a un mayor número de dimensiones, de tal forma que se habla de la curvatura en un punto en una variedad riemanniana de d dimensiones. Sin embargo, cuando la dimensión es mayor de dos, es decir, no es un plano lo que se curva sino un espacio, las posibilidades de curvatura en un punto se hacen tan complicadas que ya no pueden ser expresadas por un número sino por algo llamado el tensor de Ricci.
Un tensor no es más que la extensión del concepto de vector a dimensiones adicionales. Un escalar, un número, aparece en un gráfico como un punto, un objeto de cero dimensiones. Un vector, que tiene magnitud y dirección, aparecería en un gráfico como una línea, es decir, como un objeto de una dimensión. El tensor extiende esta idea a las dimensiones adicionales. Esto podemos interpretarlo como un conjunto de vectores relacionados, moviéndose en múltiples direcciones en un plano.
Lo veremos mejor de otra manera. En vez de pensar en un vector como un conjunto de coordenadas, lo podemos considerar una operación, es decir, un vector lo que haría es asociar una dirección a un número. Lo importante desde el punto de vista matemático es que la operación es lineal y homogénea. Gracias a esto, un vector queda completamente determinado por sus proyecciones en d direcciones, donde d es el número de dimensiones del espacio en el que se define. Por tanto, un vector se puede expresar como un conjunto de números que son en realidad sus proyecciones en un sistema de ejes coordenados.
Un vector es realmente un tensor de rango 1, asocia 1 dirección a un número. Un escalar, es un tensor de rango 0, asocia 0 direcciones a un número. Por tanto un tensor de rango 2 (un tensor ya por derecho propio), asocia dos direcciones arbitrarias a un número. Si quisiéramos expresarlo en términos de las coordenadas, como se hace con los vectores, necesitaríamos d x d números. Para un tensor de rango q, por tanto, necesitaríamos nq números.
Veamos ahora desde el punto de vista formal las ecuaciones de campo de la relatividad general. Si has llegado leyendo hasta aquí no te asustará demasiado, después de todo no es más que una igualdad tensorial en la que se relacionan un conjunto de tensores 4 x 4 (simétricos, pero en esto no vamos a entrar ahora), para un espaciotiempo de 4 dimensiones.
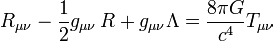
Donde Rμν es el tensor de curvatura de Ricci del que hablábamos más arriba, R es la curvatura escalar (simplificando, la curvatura entendida en el sentido que hablábamos más arriba, un número asociado a un punto del espacio), gμν es el tensor métrico (una generalización del campo gravitatorio y principal objeto de interés), Λ es la constante cosmológica, G es la constante gravitacional de Newton, c la velocidad de la luz en el vacío y Tμν el tensor de energía-impulso.
Los índices en los tensores son etiquetas, es una forma de llamarlos. En este caso se emplea la notación abstracta de Penrose. Se puede usar cualquier símbolo conveniente para los índices de los tensores. Tradicionalmente, las letras latinas se usan para indicar que se están usando coordenadas espaciales (x, y, z), mientras que las griegas se emplean para indicar coordenadas espaciotemporales (x, y, z, t). En la época de la foto esta convención no se había establecido.
Una simple observación de la ecuación de campo nos dice que podría haber algo similar con lo que escribe Einstein en la pizarra: el tensor de Ricci. Efectivamente, existe un caso especial de la ecuación de campo en el que se postula que Tμν = 0, es decir, que la energía y el momento se conservan localmente. En este caso, y por las propiedades de los tensores, sólo existe una posibilidad para que Rμν = 0 ó, usando la notación de Einstein, Rik = 0, y es que Λ = 0. En definitiva, que el pie de foto podría ser “El Dr. Einstein discutiendo [por lo de la interrogación] la posibilidad de que la constante cosmológica sea cero”.
Con esta entrada Experientia docet participa en el IX Carnaval de Matemáticas que este mes acoge Rescoldos en la trébede.
4 comentarios:
Me ha gustado mucho el post y demuestra por parte del autor una gran preparación en matemáticas y física. Qué curiosa esa confusión entre density y destiny. Gran blog el vuestro. Saludos.
Esta anécdota sobre Einstein asociada a la foto que introduce tu post de hoy es muy buena. Sensacional artículo, muy bien explicado. Una excelente aportación para el carnaval de matemáticas.
Enhorabuena
Fantástica entrada, César...y una de mis fotos favoritas de Einstein.
Saludos.
Que $latex T_\mu \nu =0$ NO significa que se conserve localmente la energía-momento. Para eso sería necesario que $\latex \nabla T_\mu \nu =0$, donde $latex \nabla $ es la derivada covariante.
Publicar un comentario